Graphenzeichnen mit gegebenen Knotenpositionen und hohen Kreuzungswinkeln

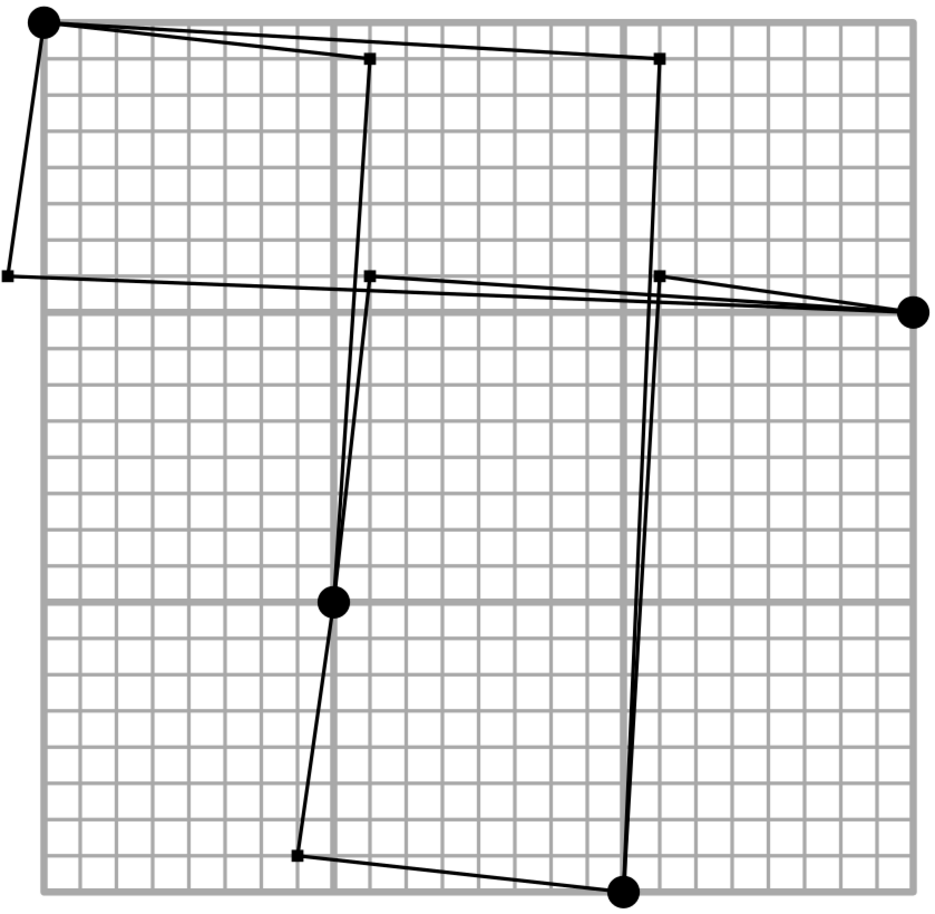
Eine häufiges Problem beim Zeichnen von Graphen ist die Einbettung auf eine gegebene Punktemenge. Hierbei ist zusätzlich zum Graphen noch eine Menge von erlaubten Knotenpositionen gegeben. In einer restriktiveren Version sind sogar die exakten Koordinaten der Knoten fixiert und es können lediglich die Kanten auf verschiedene Weisen gezeichnet werden, z.B. mit zwei oder drei Knicken. Während bisher ausschließlich Problemvarianten betrachtet wurden, bei denen die Kanten sich nicht kreuzen dürfen, wurden von Martin Fink, Jan Haunert, Tamara Mchedlidze, Joachim Spoerhase und Alexander Wolff Varianten untersucht in denen Kreuzungen von Kanten erlaubt sind, falls der Kreuzungswinkel sehr hoch ist.

Einbettungen auf Punktemengen unter der Einschränkung auf kreuzungsfreie Zeichnungen wurden schon häufiger untersucht. Es war bekannt, dass die Problemversion mit geradlinigen gezeichneten Kanten NP-schwer ist. Wie sich zeigte, gilt dies auch dann noch, wenn Kreuzungen zwar erlaubt sind, die Kreuzungswinkel aber hoch sein müssen. Es war ebenfalls bekannt, dass sich alle planaren Graphen auf alle Punktemengen entsprechender Größe einbetten lassen, wenn 2 Knicke je Kante erlaubt sind. Ist jedoch die genaue Position aller Knoten vorgeschrieben, so lässt sich die nötige Anzahl an Knicken nicht einmal für Pfadgraphen durch eine Konstante beschränken. Im Gegensatz dazu lässt sich jeder Graph mit genau festgelegten Knotenpositionen und hohen Kreuzungswinkeln zeichnen, wenn jede Kante nur einen Knick hat. Erlaubt man drei Knicke je Kante, so ist sogar eine Beschränkung auf rechtwinklige Kreuzungen möglich.

Details und weitere Ergebnisse finden sich im Konferenzartikel und den Vortragsfolien.