Übersichtliches Zeichnen von Graphen

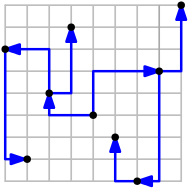
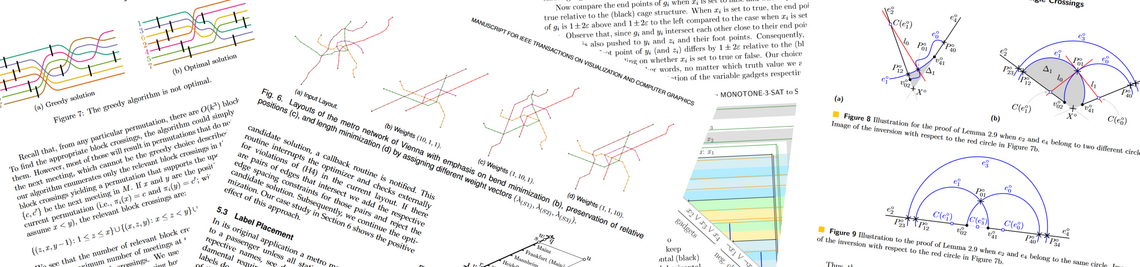
Graphen sind nicht nur ein häufiges Hilfsmittel beim Modellieren und Lösen von Problemen in der Informatik, sondern werden auch oft zur Visualisierung von Daten genutzt. Auch für Laien sind konkrete Zeichnungen von Graphen oft gut verständlich, da die Darstellung einer Verbindung oder eines Zusammenhangs durch Kanten intuitiv ist. Darüber hinaus lassen sich Methoden zum Zeichnen von Graphen auch oft für das Zeichnen realer Netzwerke, wie z.B. (U-)Bahnnetze, verwenden. Wir entwickeln und untersuchen Algorithmen für das übersichtliche Zeichnen von Graphen.

Es gibt auf dem Gebiet des Graphenzeichnens zwar schon viele beweisbar gute Algorithmen, die aber dennoch keine wirklich übersichtlichen Zeichnungen produzieren. Dies liegt daran, dass es meist schon schwer ist, nur ein gewünschtes Zielkriterium zu optimieren, wie z.B. die Anzahl der Knicke oder der Kreuzungen von Kanten. Dies führt dazu, dass andere Anforderungen an die Übersichtlichkeit einer Zeichnung nicht erfüllt werden, etwa weil die Kanten sehr lang sind oder einzelne Kanten sehr viele Knicke aufweisen. Es kann daher auch sinnvoll sein, Teilprobleme nicht optimal zu lösen, sondern gegeneinander abzuwägen. So kann eine Zeichnung besser lesbar werden, wenn es ein paar Kantenkreuzungen mehr gibt, dafür aber die Kreuzungswinkel sehr groß sind, wodurch die einzelne Kreuzung sehr viel übersichtlicher wird.

Die meisten existierenden Zeichenalgorithmen funktionieren außerdem nur auf planaren Graphen, d.h. Graphen, die sich ohne Überschneidungen zeichnen lassen. Gerade auf realen Daten basierende Graphen sind allerdings oft nicht planar. Haben solche Graphen eine gewisse Größe, was nicht ungewöhnlich ist, so sind in einer Zeichnung die einzelnen Knoten und Kanten ohnehin kaum unterscheidbar. Um die Graphen dennoch vernünftig darstellen zu können, existieren verschiedene Ansätze: man bündelt Gruppen von Kanten oder bildet Knotencluster. Es existiert jedoch noch kein Verfahren, das stets übersichtliche Zeichnungen liefert.

Projektmitarbeiter

• Alexander Wolff
• Boris Klemz
• Oksana Firman
• Johannes Zink
• Felix Klesen
• Tim Hegemann
• Marie Diana Sieper
• Jonathan Klawitter (bis 2021)
• Myroslav Kryven (bis 2021)
• André Löffler (bis 2020)
• Steven Chaplick  (bis 2020)
• Philipp Kindermann (bis 2020)
• Fabian Lipp  (bis 2018)
• Martin Fink (bis 2014)