Readable Graph Drawing
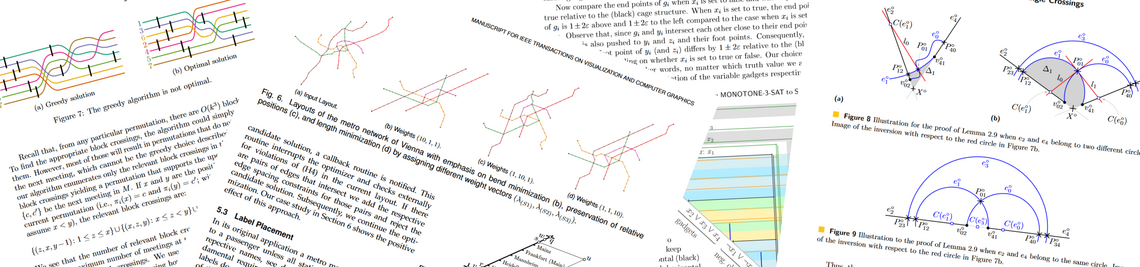
Graphs are not only a common tool for modelling and solving problems in computer science, but are also often used for visualizing data. Concrete drawings of graphs are understood also by non-experts; the representation of a link or a connection is intuitive. Moreover, methods for graph drawing can be used for visualizing real networks such as metro networks. We develop and investigate algorithms for creating readable drawings of graphs.
The literature describes many provably good algorithms for drawing graphs. Rarely, however, do these algorithms produce well-readable drawings. That is because it is often already hard to optimize only one desired criterion such as the number of bends or the number of edge crossings. This leads to other readability requirements not being fulfilled, perhaps because some edges are very long or some have many bends. It can, therefore, also make sense to do without solving partial problems optimally and rather balance several criteria against each other. A drawing can, for example, become better readable if there are slightly more crossings but all with large crossing angles.
Most existing algorithms for graph drawing work, furthermore, only on planar graphs, that is, graphs that can be drawn without crossings. Especially graphs based on real-world data are, however, usually not planar. If such graphs are large, which is not unusual, then single nodes or edges are hardly distinguishable in a drawing. There exist several approaches to draw such graphs: groups of edges are bundled or clusters of nodes are formed. So far, however, there is no method that always produces readable drawings.
Researchers
- Alexander Wolff
- Boris Klemz
- Oksana Firman
- Johannes Zink
- Felix Klesen
- Tim Hegemann
- Marie Diana Sieper
- Jonathan Klawitter (bis 2021)
- Myroslav Kryven (bis 2021)
- André Löffler (bis 2020)
- Steven Chaplick (bis 2020)
- Philipp Kindermann (bis 2020)
- Fabian Lipp (bis 2018)
- Martin Fink (bis 2014)
