Our article "Density-based Weighting for Imbalanced Regression" has been accepted for the ECML PKDD 2021 journal track

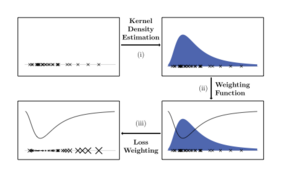
Our work deals with the problem of dataset imbalance in regression tasks and proposes a novel sample weighting approach called DenseWeight and a novel cost-sensitive learning approach based on DenseWeight called DenseLoss. Our methods allow machine learning models to be trained that focus more on performance for data points with rare target values compared to data points with more common target values. This is useful for tasks where rare cases are more important than more common cases, for example in precipitation estimation when extreme rainfall events are of particular interest.

Both the paper and the code will be made available in the next weeks.

The paper can be found here. DenseWeight is available as a python package while our experiments are also available on github.

Abstract

In many real world settings, imbalanced data impedes model performance of learning algorithms, like neural networks, mostly for rare cases. This is especially problematic for tasks focusing on these rare occurrences. For example, when estimating precipitation, extreme rainfall events are scarce but important considering their potential consequences. While there are numerous well studied solutions for classification settings, most of them cannot be applied to regression easily. Of the few solutions for regression tasks, barely any have explored cost-sensitive learning which is known to have advantages compared to sampling-based methods in classification tasks. In this work, we propose a sample weighting approach for imbalanced regression datasets called DenseWeight and a cost-sensitive learning approach for neural network regression with imbalanced data called DenseLoss based on our weighting scheme. DenseWeight weights data points according to their target value rarities through kernel density estimation (KDE). DenseLoss adjusts each data point’s influence on the loss according to DenseWeight, giving rare data points more influence on model training compared to common data points. We show on multiple differently distributed datasets that DenseLoss significantly improves model performance for rare data points through its density-based weighting scheme. Additionally, we compare DenseLoss to the state-of-the-art method SMOGN, finding that our method mostly yields better performance. Our approach provides more control over model training as it enables us to actively decide on the trade-off between focusing on common or rare cases through a single hyperparameter, allowing the training of better models for rare data points.